Printable version

Transformations & Symmetry - Lesson 1-6

Today, we went over a lot of notes! We started with the following warmup:

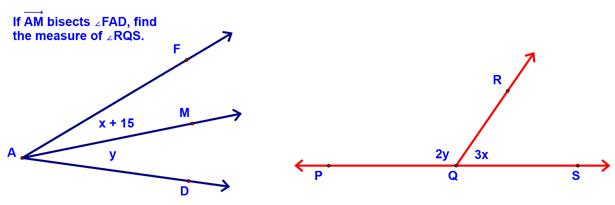
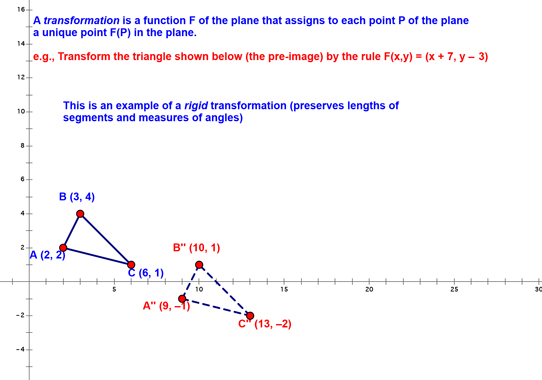
Hopefully, you can find the measure of the angle to be 90°!

We then started the lesson...we started by defining a rigid transformation and showing an example:

Next, we talked about a non-rigid transformation and showed an example...something called a dilation.

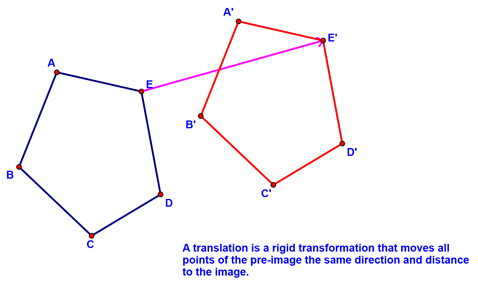
At this point, I told you that we would only be studying rigid transformations this year! Of these, there are three types you'll need to know: translations, rotations, and reflections. We started by defining a translation:

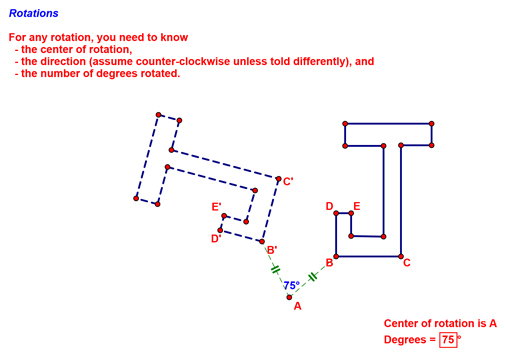
Next, we moved to defining rotations. For these, we noted a few things we needed to know:

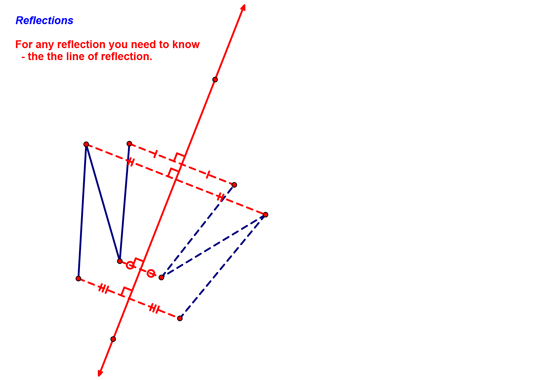
We then discussed reflections. For these, we needed a pre-image and a line over which we could reflect!

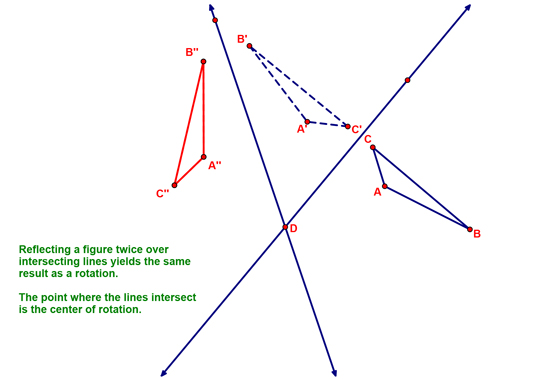
Next, I showed you how two reflections, over intersecting lines, give the same result as a rotation! Can you determine the degree the pre-image was rotated to form the image here? (It's 117°)

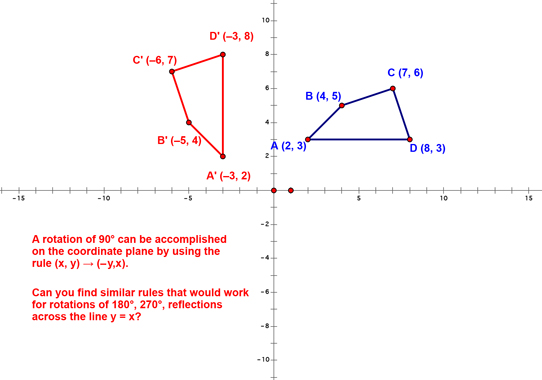
Next, we talked about some special rules that you can use when performing some transformations on the coordinate plane:

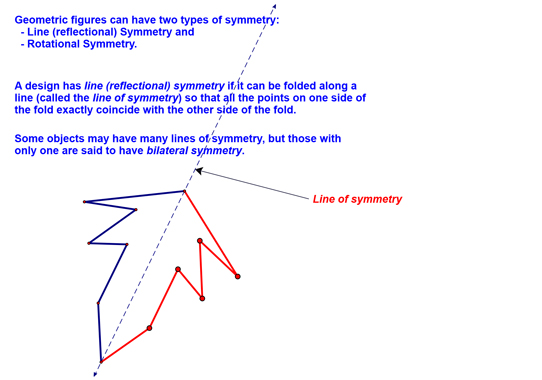
The other rules, in case you were wondering, are (x, y)-->(-x, -y) for 180° rotation, (x, y)-->(y, -x) for 270° rotation and (x, y)-->(y, x) for a reflection across the line y = x.

At this point, we discussed different types of symmetry...starting with line symmetry:

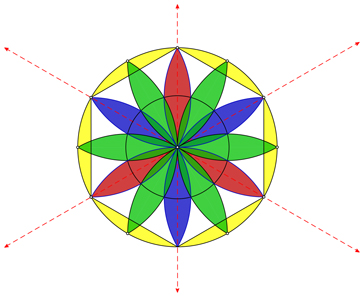
We FINALLY wrapped up by discussing rotational symmetry:

Notice that the first example above has 120° rotational symmetry and the second example has point symmetry (180° rotational symmetry).

Whew! That was a lot for one day!