Printable version

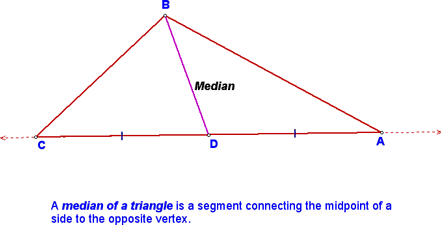
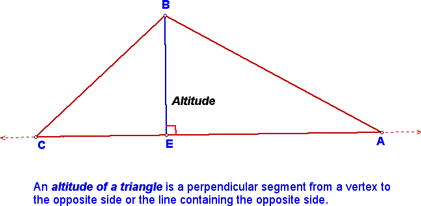
Beyond CPCTC - Lesson 3-4

We began today by learning a couple of new definitions:

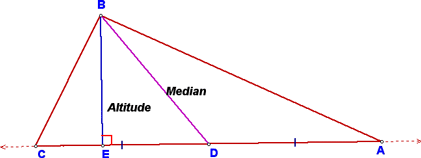
Note that these are not the same thing, as can be seen by the diagram below:

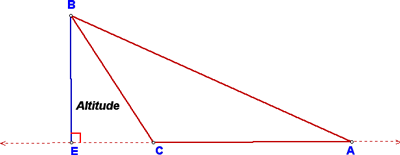
Also note that an altitude can be outside the triangle (if the triangle is obtuse):

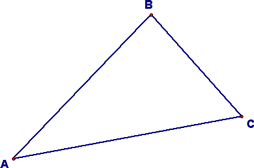
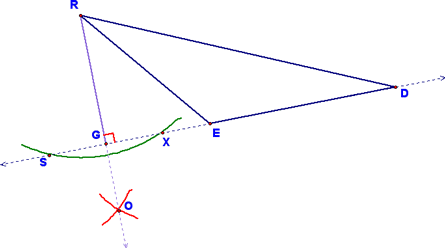
You should also know that there are three altitudes and medians in any triangle.

Next, we learned how to construct these!  We started with constructing a median.  In order to do that, we started with a triangle (any triangle will do):

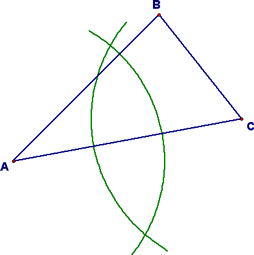
We then constructed the perpendicular bisector of segment AC.  To do this, we first made "the fish."

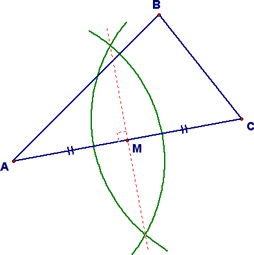
From here, we found the midpoint, M, of the segment AC.  Please note that you don't have to draw in the whole perpendicular bisector, if you don't want.  Just line up your straight edge as if you were going to draw it in and use this to locate point M.  Also note that we've correctly marked the diagram to indicate that M is the midpoint of segment AC.

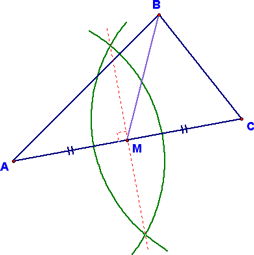
From here, it's easy to complete the construction.  Just draw in the median BM using your straight edge!

Then, we constructed an altitude of an acute triangle. We did this using the construction of a perpendicular to a line from a point not on the line.

Finally, we used the same construction to construct an altitude for an obtuse triangle.  The only trick here is that you need to extend the side opposite from the vertex in order to make the perpendicular.  Hopefully, you can replicate the steps required here!

At this point, we talked about how and when to use "auxiliary lines" in our proofs:

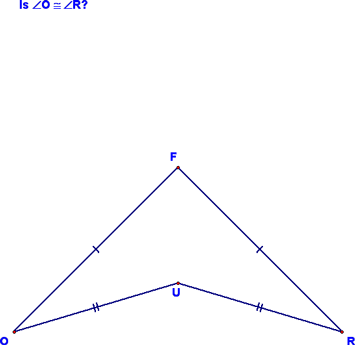
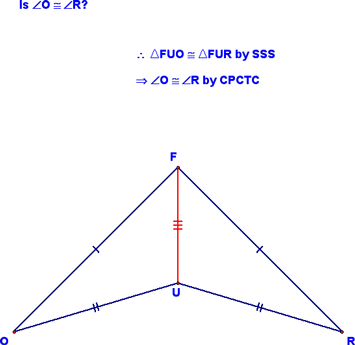
We went through a couple of examples of how this might be used:

It turns out that this problem can be solved if you first draw in segment UF:

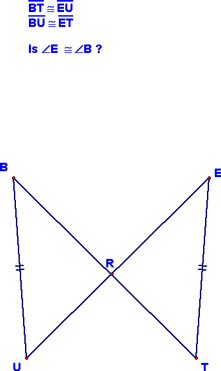
The next example looked like:

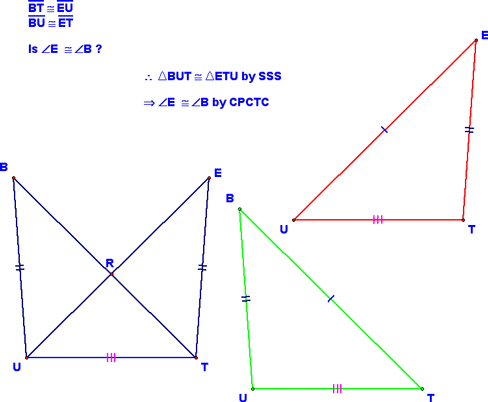
This can be solved by first drawing in segment UT....I then showed you how the overlapping triangles could be "pulled out" (the red and green triangles below) to show how they are congruent.

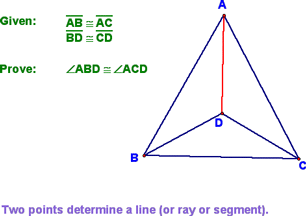
And finished with an example proof...note that the diagram didn't start with segment EG in it...we added that using Auxiliary Lines.