|
| you are here > Class Notes - Chapter 3 - Lesson 3-2 | |||||||||||||||||||||||||||||||||||
|
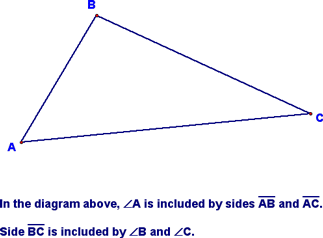
Three Ways to Prove Triangles Congruent - Lesson 3-2 Today, we started by making sure that we understood what an included angle or included side was:
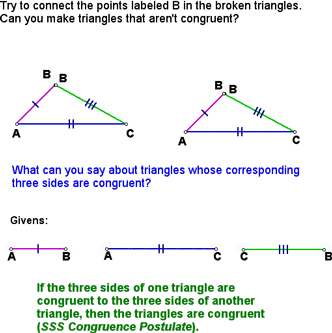
Now in a triangle, there are 3 sides and 3 angles, so this implies that to prove that two triangles are congruent, we'd have to prove that all three corresponding sides and all three corresponding angle were congruent. However, we soon discovered that there are some shortcuts for proving congruence. The six possibilities (remember that we eliminated the possibilities that included only one part of corresponding triangles and two parts of corresponding triangles), which we could use are:
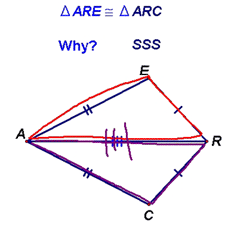
Given this, we started to look at these possibilities, starting with SSS, which we determined was a shortcut for proving triangle congruence since, when given three fixed sides, we could only create congruent triangles.
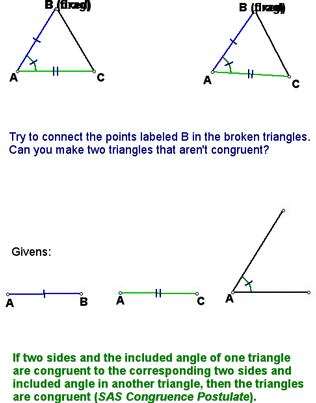
Next, we looked at SAS, which also helps us to prove triangle congruence:
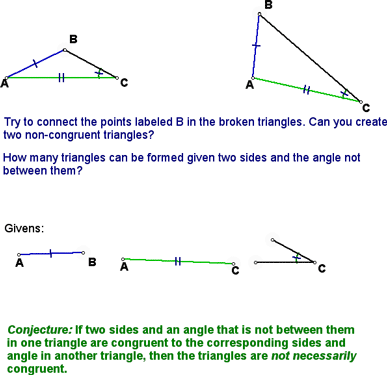
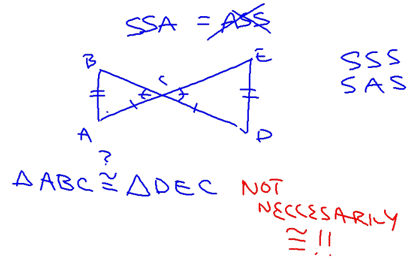
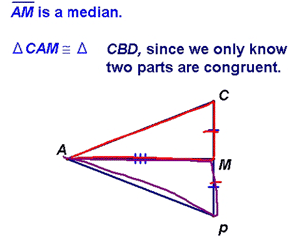
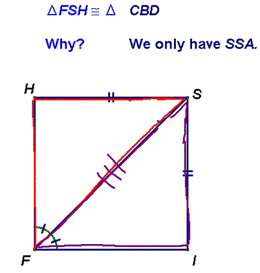
Next, we looked at the SSA case. This one didn't work (see below). Remember the difference between SSA and SAS. In the latter, the angle is directly between the two sides, whereas in the former, the angle is not directly between the two sides.
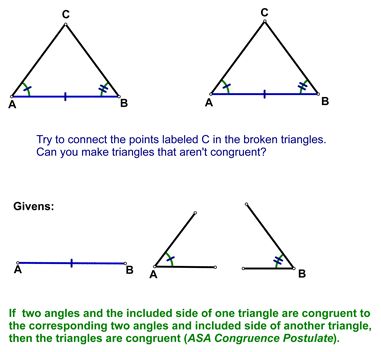
We also looked at ASA:
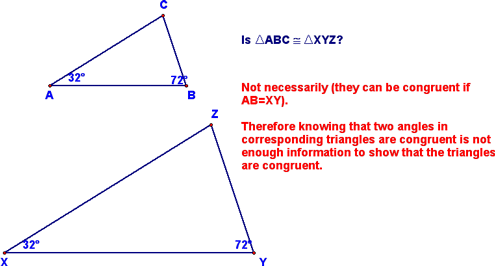
We also looked at the AAA case, which we had already agreed didn't work:
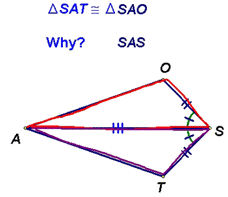
Here are some examples. You should be able to see why the first doesn't work (SSA) and why the second does (SAS) for proving congruence:
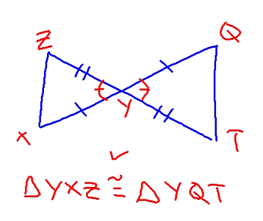
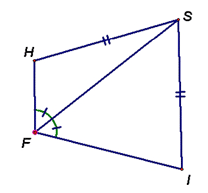
You should be able to why this is true by looking at the following diagram, which has the same limitations, but clearly shows two non-congruent triangles:
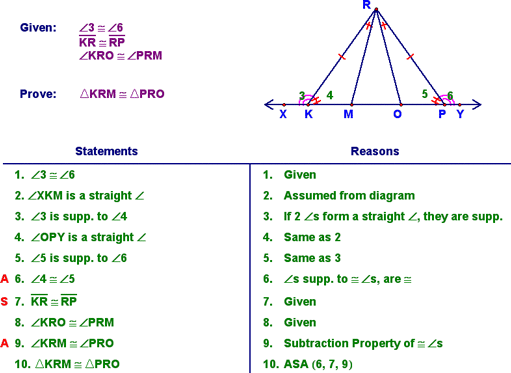
Finally, we went through an example proof...you should be able to follow this!
|
|
||||||||||||||||||||||||||||||||||