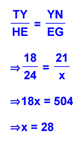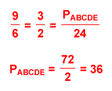Printable version

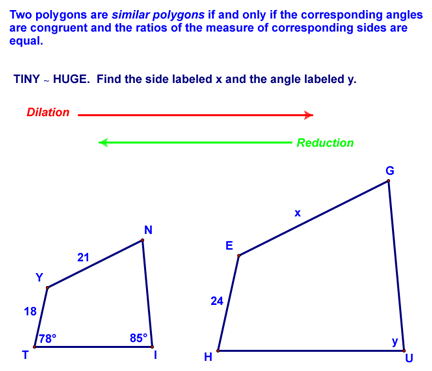
Similarity - Lesson 8-2

Today, we found out that ratios were very important when we began discussing similar polygons. First, we defined what these were:

Looking at the example above and understanding that corresponding sides are proportional helps us to set up the following equation to find side x.

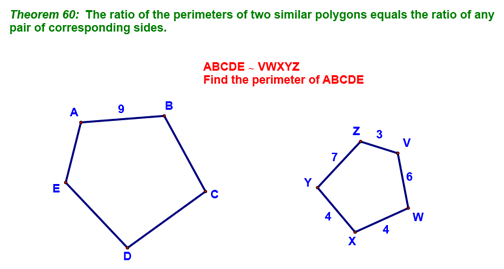
y is easy to find assuming that you understand that corresponding angles of similar polygons are congruent. Angle M corresponds to angle I (you should know this from the order of the letters in the statement of similarity (SMAL ~ BIGE), so angle I, or y, must be the same as angle M, or 85 degrees.

Next, we covered the following theorem, which relates the ratio of the sides to the ratio of the perimeters of similar polygons:

For this problem, you should first note that side AB corresponds to side VW, so the ratio of the sides is 9/6 or 3/2. Therefore, we can calculate the perimeter of ABCDE in the following manner:

Finally, we talked about how to find the 1st, 2nd, 3rd, or 4th proportional of three given numbers:

That was it for today!