|
| you are here > Class Notes - Chapter 10 - Lesson 10-4 | |||||||||||||||||||||||||||||||||||||
|
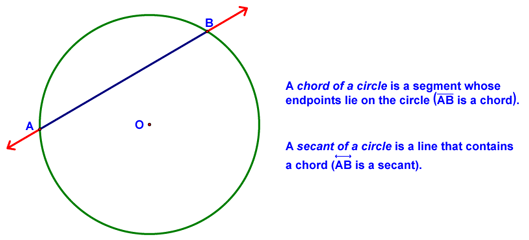
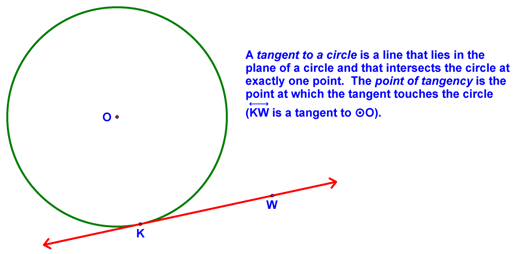
Secants and Tangents - Lesson 10-4 Today we began by looking at the definition of chords, secants, and tangents of a circle:
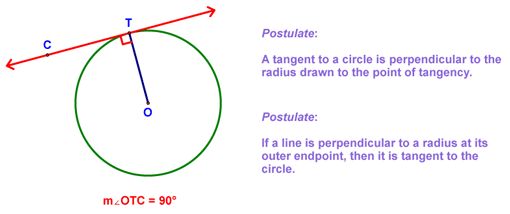
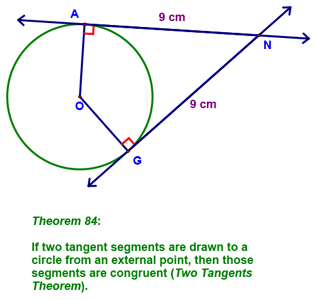
We then discovered a property of tangents:
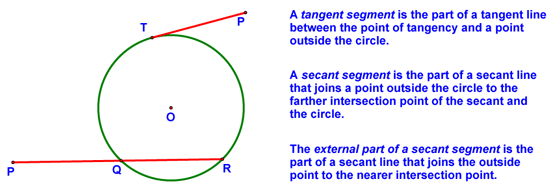
Next, we defined tangent segments and secant segments:
Next, we learned a property of tangents:
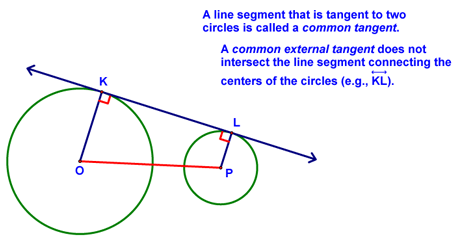
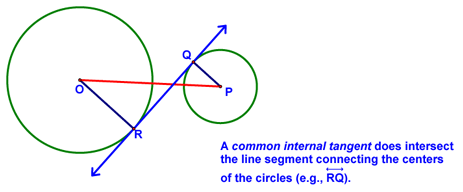
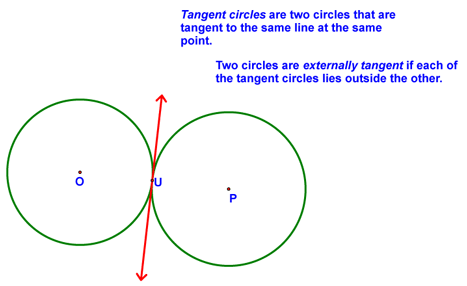
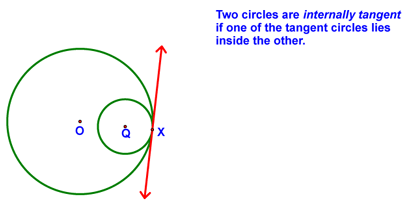
We then covered a number of additional definitions:
We finished by talking about the Common Tangent Procedure (detailed below) and doing the following example...make sure you can follow these steps for either a common internal or common external tangent!
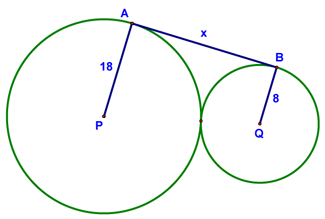
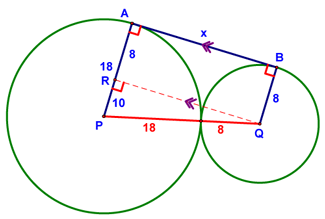
The problem was to find x in the diagram below:
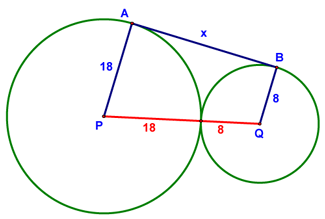
Step 1 is to draw in the segment connecting the centers of the circles (shown in red below):
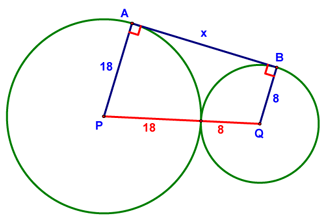
Step 2 is to draw in radii to the points of tangency of the common tangent. These were already drawn for our example (segments AP and BQ), but for now, let's at least note that they form right angles with the common tangent segment.
Step 3 is to use the parallel postulate to draw in a line parallel to the tangent through the center of one of our circles (segment RQ). Note that ARQB is a rectangle, so its opposite sides are congruent. Using this fact and a little simple math, we can see that RP = 10.
Step 4, the last step, uses the Pythagorean Theorem (or a family of right triangles - in this case we have a 5-12-13 triangle), solve for the length of segment RQ, which is the same as x!!
Note that this procedure (Steps 1 - 4) will also work for finding the length of a common internal tangent. The picture will be different, but the result will be the same! |
|
||||||||||||||||||||||||||||||||||||