Chapter 10 Class Notes

you are here > Class Notes - Chapter 10 - Lesson 10-8

Printable version

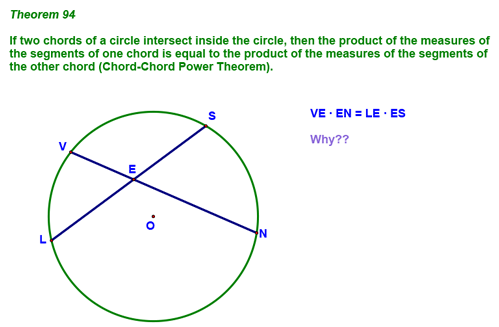
The Power Theorems - Lesson 10-8

Today we learned a number of cool theorems (called the Power Theorems...sounds cool, huh?) that are based on similar triangles. The first is shown below and should be pretty straight forward to understand if you look at proving the two triangles similar (which, of course implies that corresponding sides are proportional):

Theorem 94 - The Chord-Chord Power Theorem

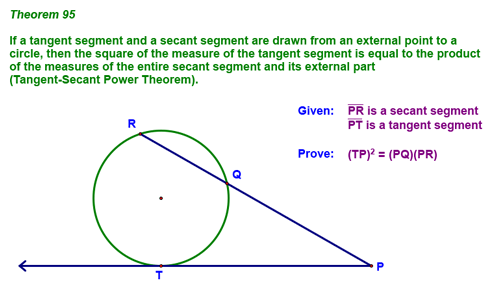
The second power theorem is show below:

Theorem 95 - The Tangent-Secant Power Theorem

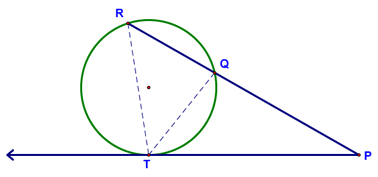
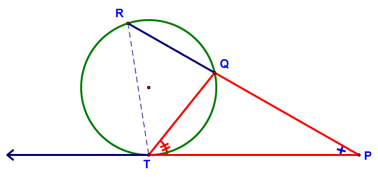
roving the Tangent-Secant Power Theorem is a little more difficult, but still involves similar triangles. The key is to draw in the two auxiliary lines shown below (segment RT and segment QT):

Step 1 for Proving The Tangent-Secant Power Theorem

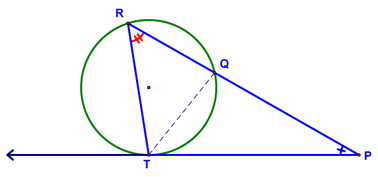
Note that angle R and angle QTP are congruent (why?) and that angle P is in both triangles RTP and QTP. With this information, you should see that the triangle below (Triangle RTP)

Step 2 for Proving The Tangent-Secant Power Theorem6

and the the triangle TQP shown below are similar.

Step 3 for Proving The Tangent-Secant Power Theorem

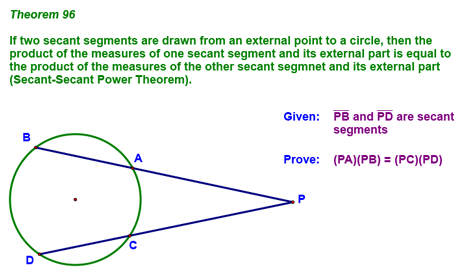
Since , this implies that or (TP)2 = (PR)(PQ). Woohoo!

The last power theorem (the Secant-Secant Power Theorem) is shown below:

Theorem 96 - The Secant-Secant Power Theorem

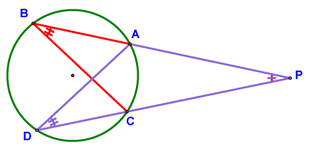
This theorem is proved using the two triangles shown in the diagram below. You should be able to figure this one out!

Hint for proving The Secant-Secant Power Theorem

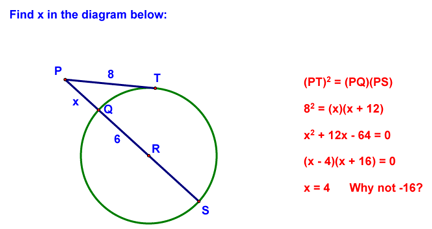
We finished by doing the following example problem and then reviewing homework:

Example Problem