Printable version

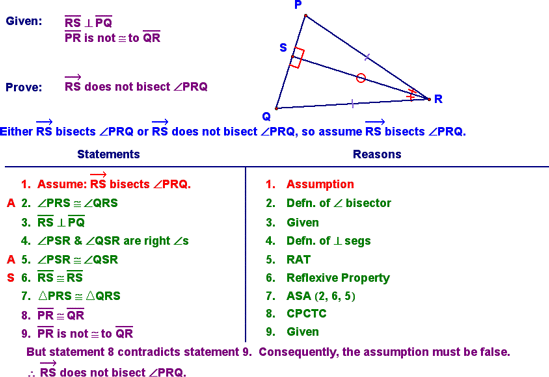
Indirect Proof - Lesson 5-1

Today, we learned how to do the formal structure of indirect proof. We started with the following example, which shows how we always start an indirect proof by assuming the opposite of what we're trying to prove. We then use this, in addition to some given information, to try to contradict one of the givens. If we can do that, then we know our assumption was erroneous, and that the opposite of our assumption (the thing we're trying to prove) is true!

Note again, that we started by looking at the "Prove" statement and assumed the opposite of it. That is the key to doing indirect proofs. Start with the opposite of what you're trying to prove and try to contradict one of the other givens. We stated the procedure as shown below:

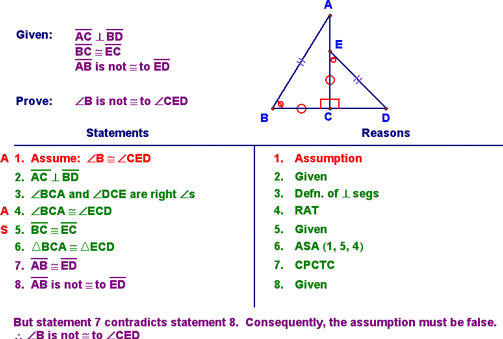
We then did the following example to solidify how to do this type of prove. This is the way I'd like to see you do these types of proof. The concluding "paragraph" should always say "Statement x contradicts statement y. Consequently, the assumption must be incorrect. Therefore, [Prove statement goes here]!"

Given some of the really hard detour proofs we've been doing, this really isn't that bad. Just make sure to get the procedure down and the proofs should be relatively straight forward.