|
| you are here > Class Notes - Chapter 5 - Lesson 5-3 | |||||||||||||||||||||||||||||||||
|
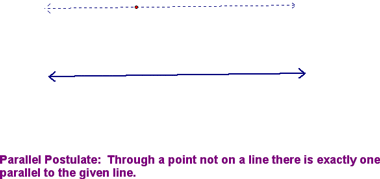
Congruent Angles Associated with Parallel Lines - Lesson 5-3 Today, we started by covering the following postulate:
This postulate helped us to prove the following theorem. The key thing here to understand is that if angle 1 is not congruent to angle 2, then there has to be a line other than a that goes through point P that is parallel to line b (because of the Parallel Postulate). Once you understand that, the rest follows.
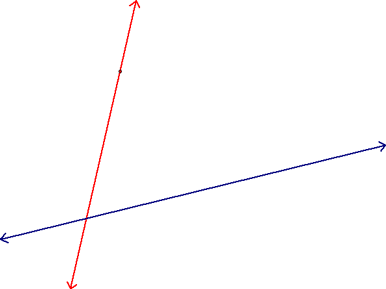
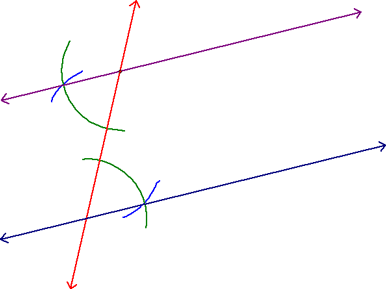
We then used this postulate along with the AIP theorem to construct parallel lines using the Alternate Interior Angles Method. For this, you start with a given line and a given point not on that line:
Next, you use your straight edge to construct a second line that goes through both the given point and the given line. This can be done at any angle.
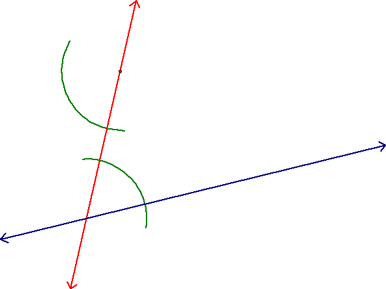
Now, center your compass at the point where these two lines intersect and draw an arc that crosses both legs of the angle.
Using the same radius as in the previous step, center your compass at the given point and construct an arc that crosses the red line and the place where you think the parallel line will be.
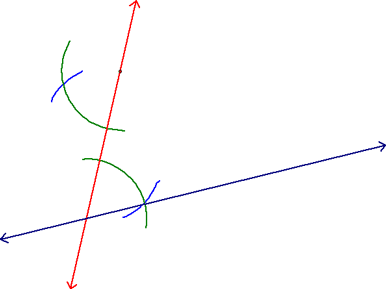
Now, center your compass at the point where the first arc crosses the red line. Set the radius to the distance from here to the point where the first arc crosses the given line. Draw an arc (the only reason to do this is to make sure you have the distance correctly set).
Using the same radius as the previous step, center your compass at the point where the second green arc crosses the red line. Make an arc that crosses the second green arc.
You're there! Now you just have to use your straight edge to connect this new point with the given point. You now have parallel lines (the given line and the purple line). Do you see how we created them? Right...we constructed congruent alternate interior angles!
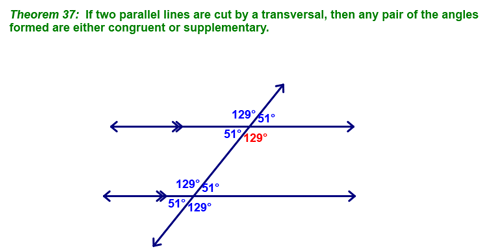
At this point, we recognized that parallel lines with a transversal really give us a lot of information. We started with the following:
And then moved on to these theorems (most of which are the converses of ones we did yesterday).
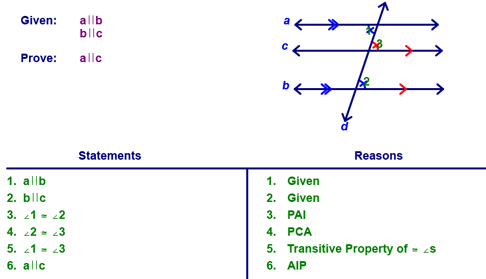
We concluded by proving Theorem 43. This should be pretty straight forward for you by now!
|
|
||||||||||||||||||||||||||||||||