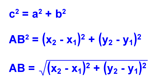|
| you are here > Class Notes - Chapter 9 - Lesson 9-5 | |||||||||||||||||||||||||||||||||||||||||
|
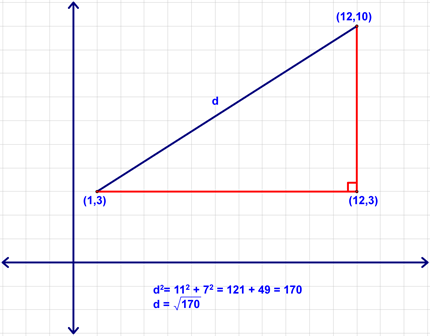
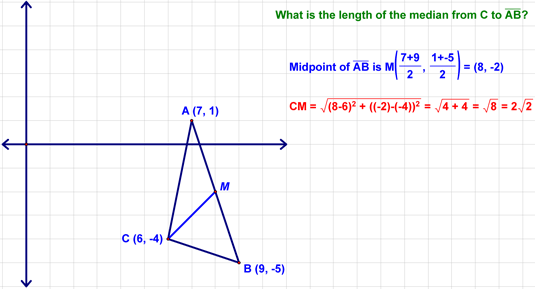
Lesson 9-5 - The Distance Theorem Today, we used the Pythagorean Theorem to derive one of the more useful formulas in geometry - the Distance Formula. The key here is to remember that if you're asked to find the length of a line segment in the Coordinate Plane (e.g., you will be given the coordinates of the endpoints), you can always make a right triangle and use the Pythagorean Theorem to find the length of the hypotenuse! Let's see what I mean. We started by looking at the segment with endpoints (1,3) and (12,10). Let's begin by making a right triangle here with our segment as the hypotenuse (see below). Now, figuring out the lengths of the legs is easy, right? Using those lengths and the Pythagorean Theorem (a2 + b2 = c2), we can find the length of the segment (d in this case).
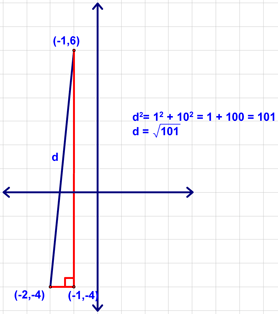
Let's do it again to make sure we've got it. To find the length of the segment with endpoints (-1,6) and (-2,-4), we start by making a right triangle with this segment as the hypotenuse. Now use the lengths of the legs (1 and 10 in the example below) and the Pythagorean Theorem to calculate the length of the hypotenuse.
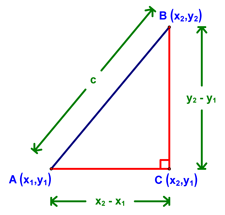
Now, let's generalize. Assume that we have a segment AB somewhere on the coordinate plane with endpoint coordinates (x1,y1) and (x2,y2), respectively (see the diagram below). The coordinates could be anything, even A (9999,-2001) and B (-2539,122233445)! Let's go through our process again. First, we draw a right triangle with our segment as the hypotenuse. Next, we find the length of AC and BC. You should be able to see that these are x2 - x1 and y2 - y1, respectively (see below).
Now, using the Pythagorean Theorem with AC as a, BC as b, and AB as c, we get the following result:
This can be summarized with the following theorem:
At this point we did a couple of examples using our new formula. Note that you can choose either endpoint to be (x1,y1) or (x2,y2). It works out to be the same either way (in the example below, I first use (8, 15) as (x2,y2) and (-7, 23) as (x1,y1) on the left, then flip it and use the opposite on the right)!
Another couple of examples followed:
|
|
||||||||||||||||||||||||||||||||||||||||