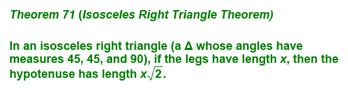|
| you are here > Class Notes - Chapter 9 - Lesson 9-7 | |||||||||||||||||||||||||||||||||||||||||
|
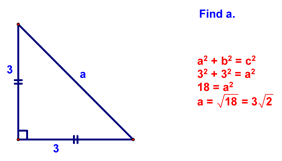
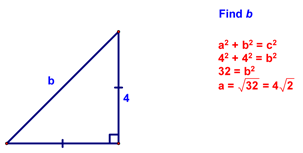
Lesson 9-7 - Special Right Triangles OK, so I don't say this often, but I really mean it today...this could be one of the most important lessons we have all year. You'll use the results of this lesson more than almost anything else you learn this year. Granted, most of this use will be on other math problems throughout your high school and college careers, but let's face it...if you learn it now, you'll do better later! We started today's lesson by looking at the following examples of problems involving isosceles right triangles:
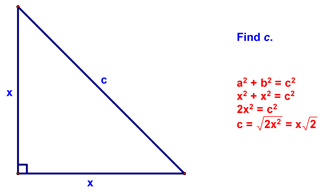
At this point, I asked if anyone noticed a pattern and a few of you did. The result is shown below:
This, in turn, leads to the following theorem:
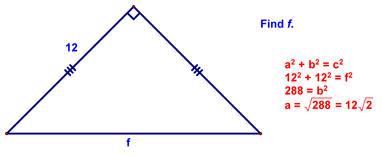
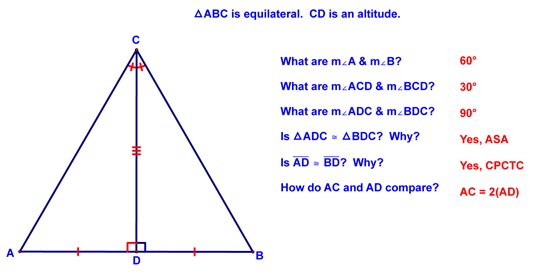
Next, we looked at 30-60-90 (a.k.a. 30-60-Right) triangles. To do this, we first looked at an equilateral triangle, from which we were able to derive some interesting facts about a 30-60-90 triangle:
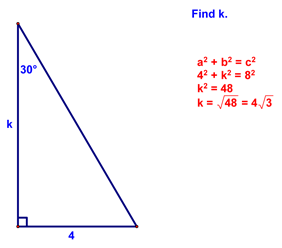
You should be able to see how we came up with the last conclusion - if you can't follow it through step by step until you can! We then looked at the following example:
Why did we know the hypotenuse was 8? If you don't know, then look at the previous diagram and figure it out!! At this point, we generalized in the following theorem:
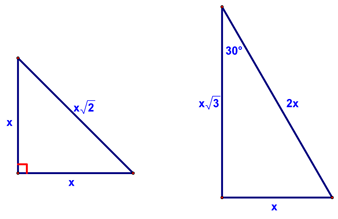
To conclude, we drew the following two special triangles. Please, please, please....memorize these!! If you do, you'll thank me many times over the next couple of years...
|
|
||||||||||||||||||||||||||||||||||||||||