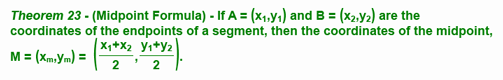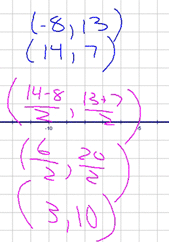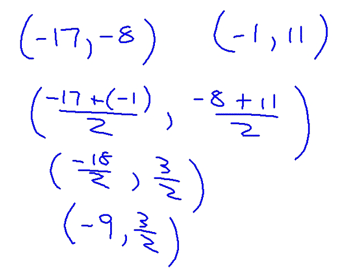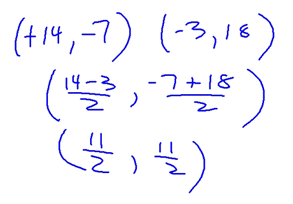Printable version

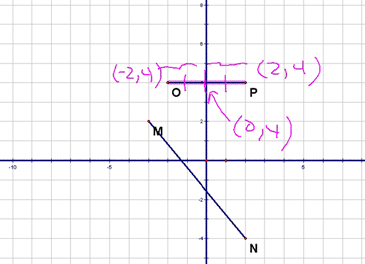
Detours and Midpoints - Lesson 4-1

Today, we formally went through an explanation of something we've been doing for a while.  It's called "proofs with detours."  You should be getting pretty comfortable with these by now...you have to prove one (or more) sets of triangles congruent in order to get enough information to prove other triangles (or parts thereof) congruent.  Here's an example:

There were plenty of other examples on last night's homework...make sure you understand all of these (some of the harder ones are shown below)!

We then went over how to find the midpoint of a segment given it's endpoints.  This should be pretty straight forward for you...

We came to the conclusion that finding the midpoint of a line segment given it's endpoint's coordinates, was as easy as finding the average of the x values and the average of the y values.

As an example, I asked you to find the midpoint of the segment whose endpoints were at (-8, 13) and (14, 7) - It can be done by simply using the formula I gave you above.  Set -8 and 13 to x₁ and y₁, respectively and 14 and 7 to x₂ and y₂, respectively.  Plug them in and you're all set!

Here are a couple of more examples of using this formula:

and...

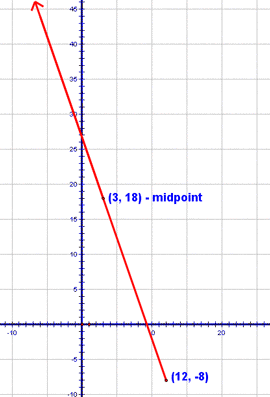
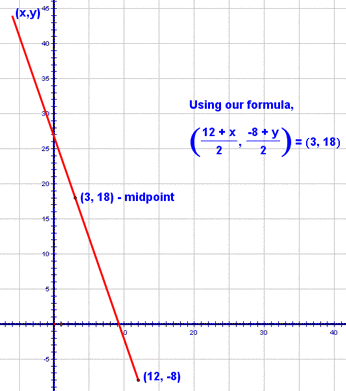
Here's one that's a little different.  In this one you're told that one endpoint of a segment is (12,-8) and that the midpoint is (3,18) and your task is to find the other endpoint.  To start this problem, let's see what this would look like on a graph:

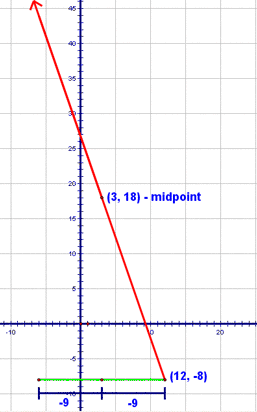
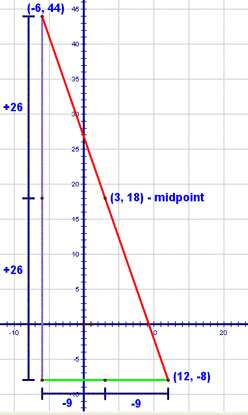
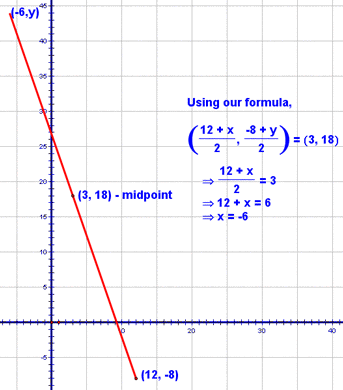
So, our other endpoint is somewhere along that red ray, right?  There are two ways to approach this problem.  The first is to think about the horizontal and vertical movements separately.  Let's think about the horizontal movement first.  To get from an x coordinate of 12 to one of 3, I have to go 9 spaces to the left.  Now, wouldn't it make sense that to get from the midpoint to the other endpoint, I'd have to go 9 more spaces to the left?  Let's see, 12 - 3 = 3 and 3 - 9 = -6.  So, the x-coordinate of the other endpoint, must be -6!

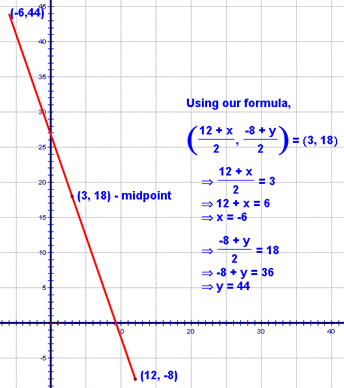
Let's apply the same process to finding the y-coordinate of the other endpoint.  We're starting at a y coordinate of -8 and when we get to the midpoint, we're at a y-coordinate of 18.  So...to get from -8 to 18, we add 26, right?  That must mean that to get from the midpoint to the other endpoint, I've got to add 26 to the y-coordinate of the midpoint.  So, 18 + 26 is 44!

Alternatively, we could also solve this problem algebraically.  Start by giving the other endpoint the coordinates (x, y).  Then, use the midpoint formula:

You should be able to see how the following is then true for the x-coordinate of the other endpoint:

The y-coordinate can be found in the same manner:

That's it for today...the midpoint stuff should be straight forward, but the detour proofs require a lot of practice, so make sure you do it...