Printable version

The Equidistance Theorems - Lesson 4.4

We started today with the following warmup problem...It is a good application of the theorem we learned yesterday, so make sure you can do something similar to this!

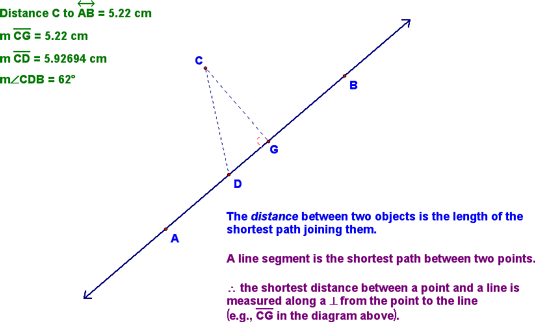
We then talked about a number of things, starting with the way to measure the distance between a point and a line...

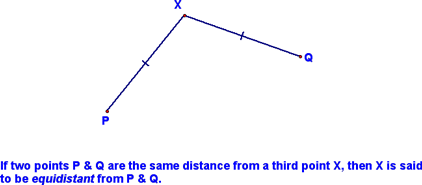
At this point, we defined the term equidistant:

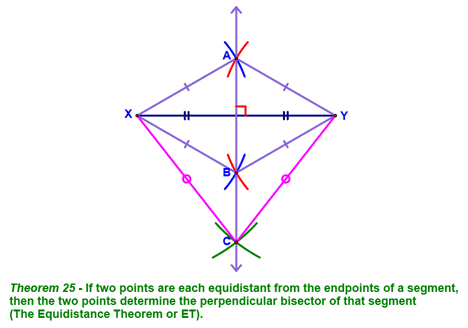
We then looked at two theorems that we first justified by doing a couple of constructions.  For the first one, we started by defining the perpendicular bisector of a segment.  We constructed this as show below (points A & B).  We then recognized that we could have constructed point C, which is also equidistant from points X & Y, although at a different distance.  This allowed us to come to the conclusion shown in Theorem 24 (The Equidistance Theorem).

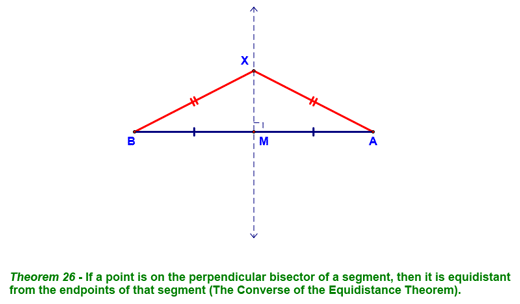
We then talked about the converse of this theorem...what if you already have the perpendicular bisector?  What do you know about any point on it?

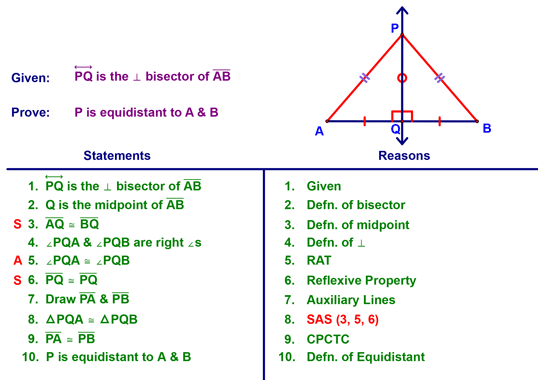
As always, I thought it might be worth doing the formal proof for one of these.  You should be able to come up with this diagram, givens, prove statement, etc. just from the theorem!!

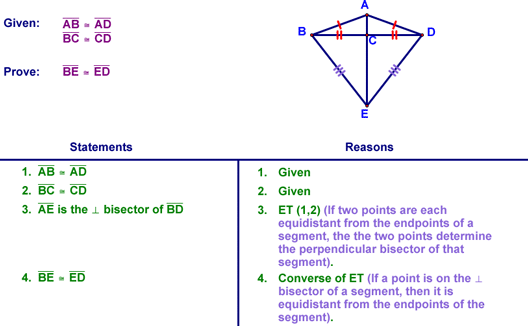
We concluded by using these theorems in a proof....gee...isn't it much shorter to do it this way, then to have to do all the steps that would be required otherwise?  Also note that you'll often see these two theorems (ET and Converse of ET) used in combination like this in proofs. For those of you who hate writing long theorems in proofs (is there anyone who likes that?), you'll be glad to know that all you need to write is the part in green!